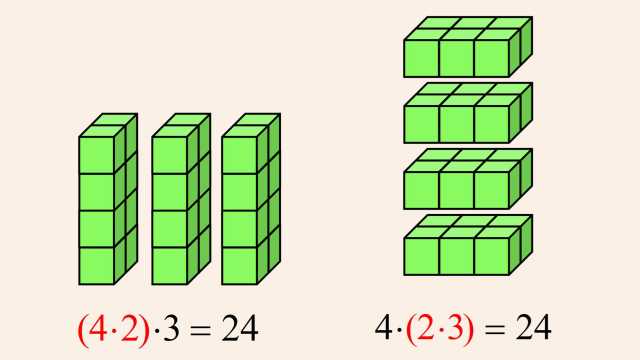
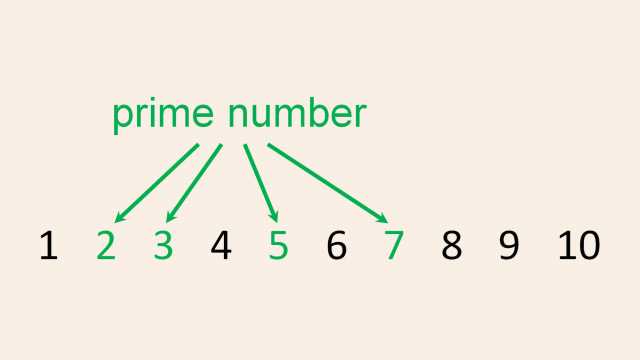
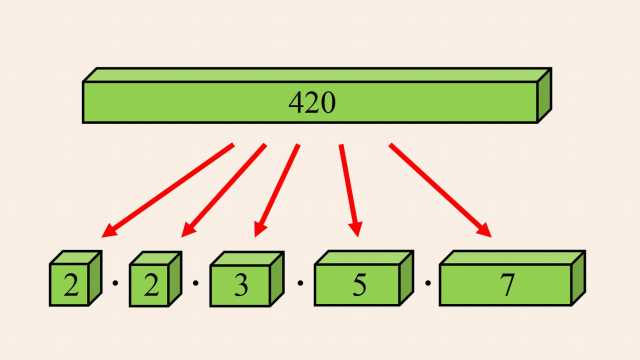
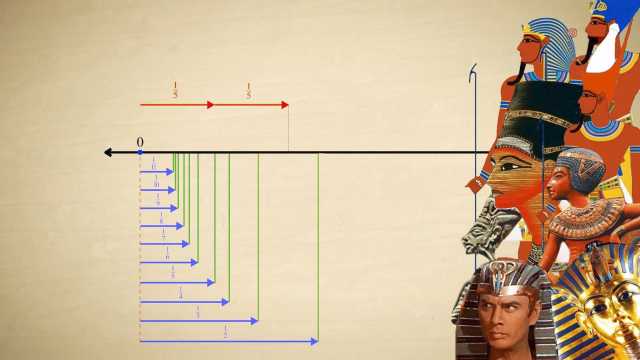
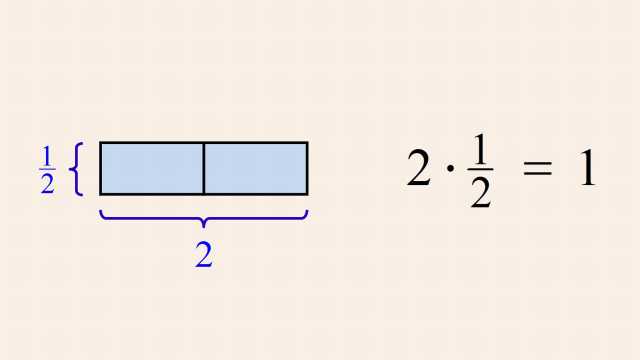
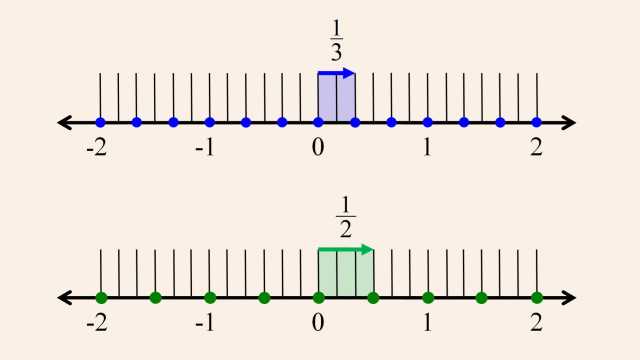
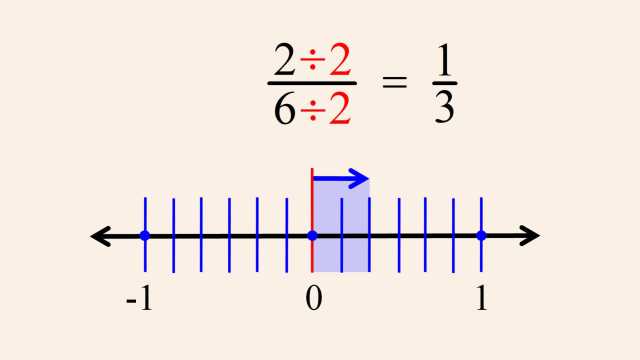
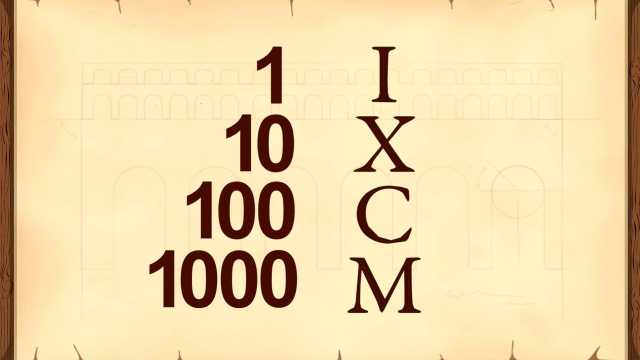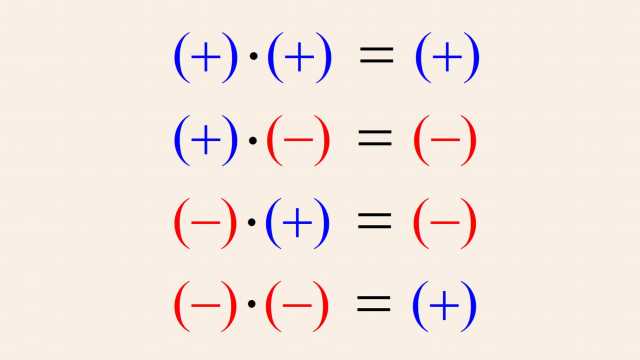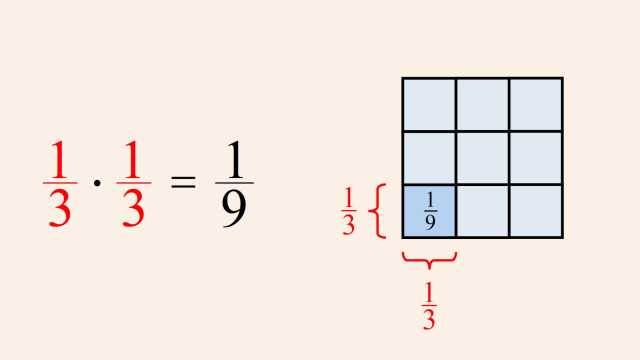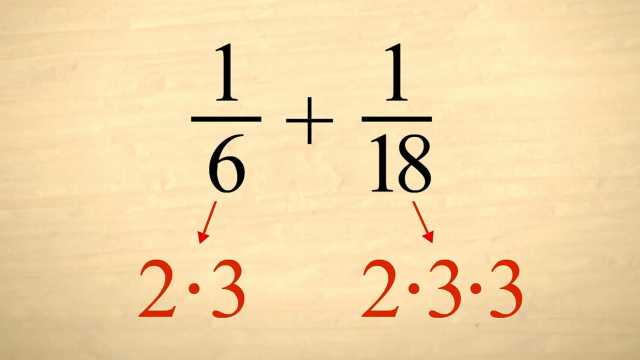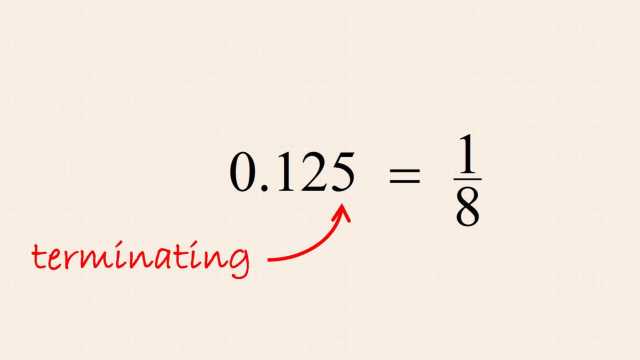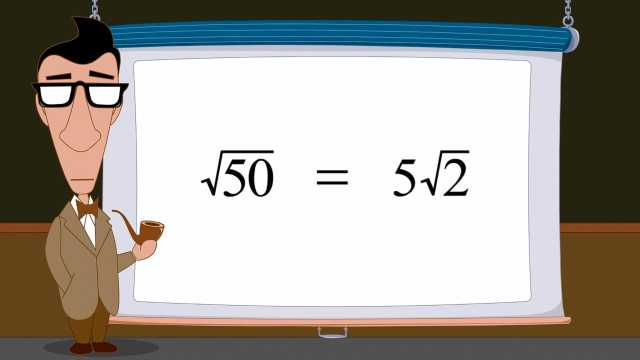4. Whole Numbers, Integers, and the Number Line
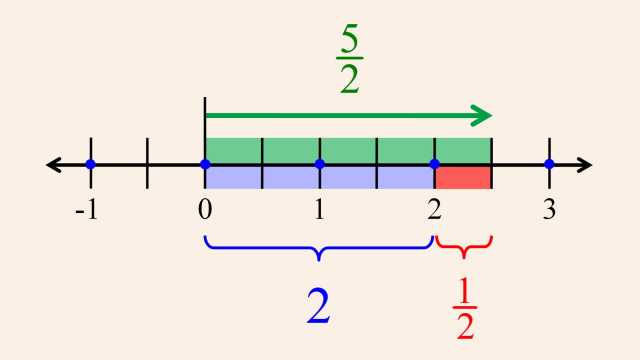
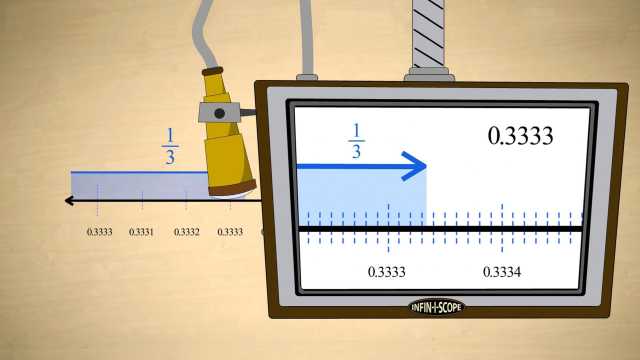
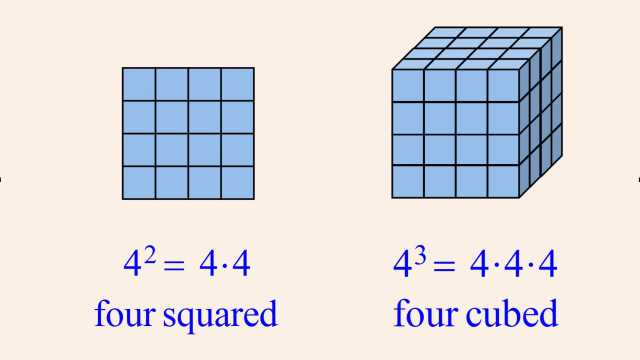
Number systems evolved from the natural 'counting' numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line.