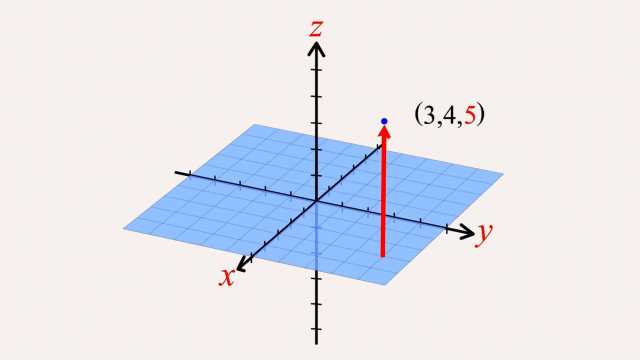
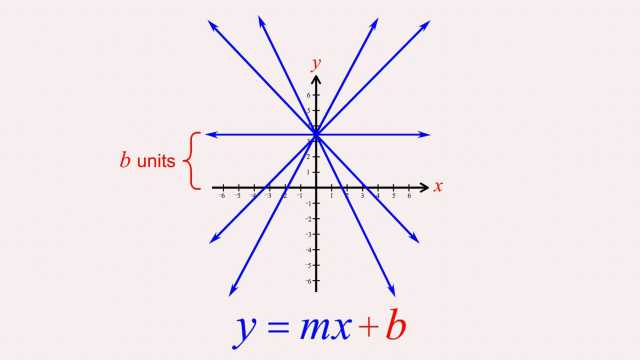
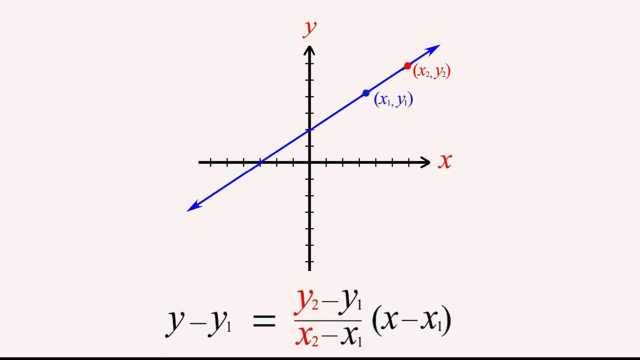
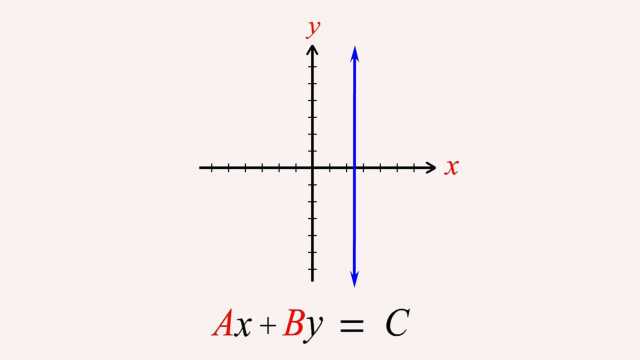
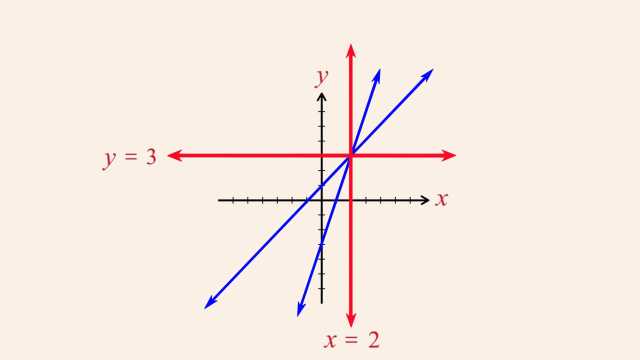
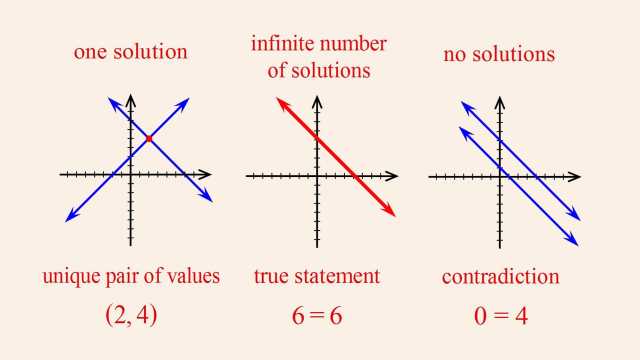
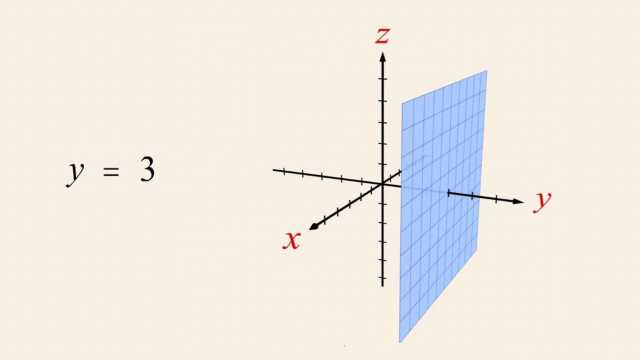
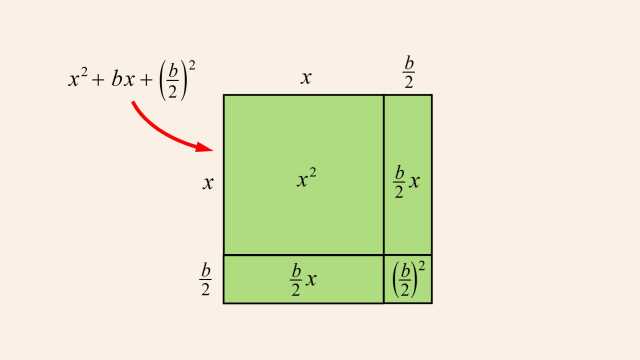
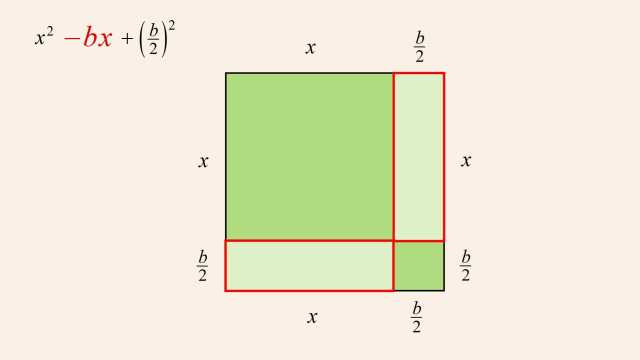
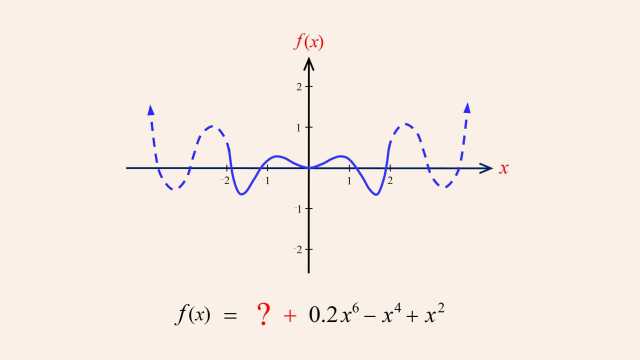
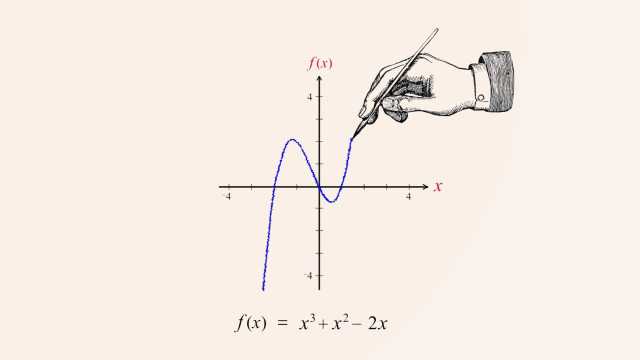
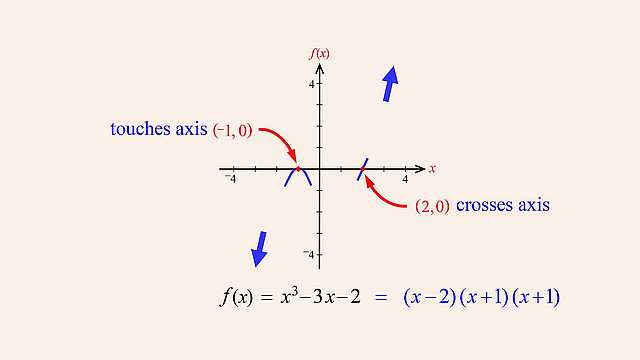
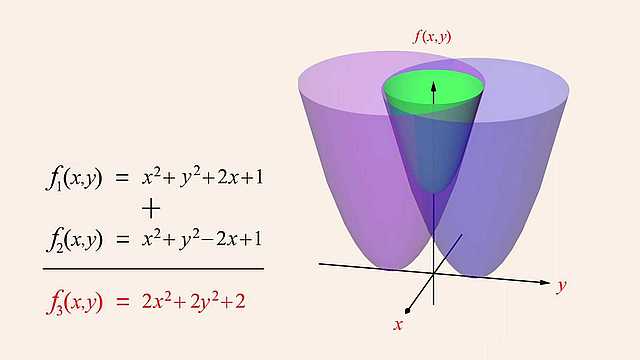
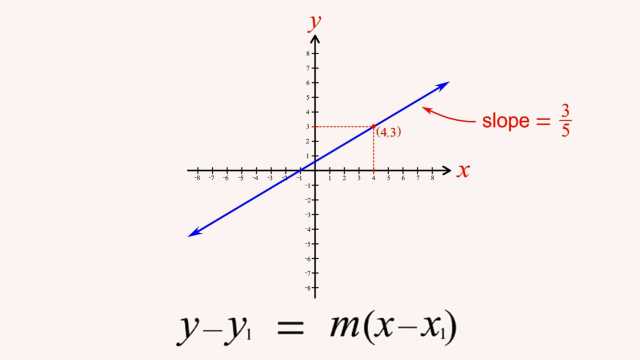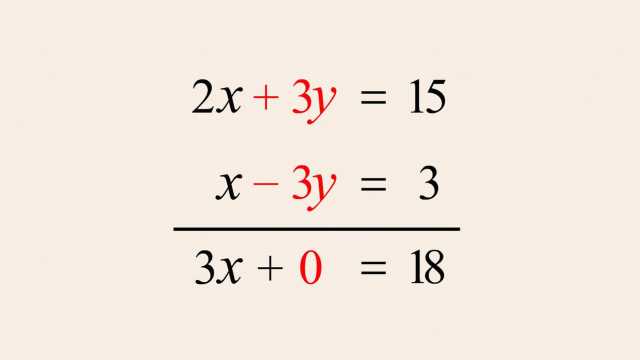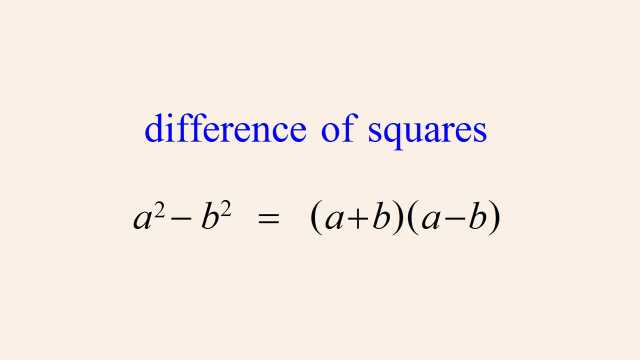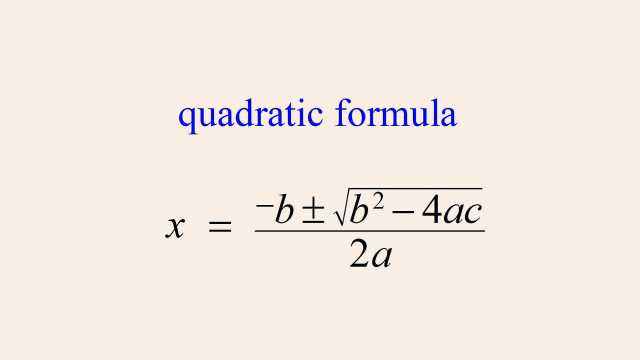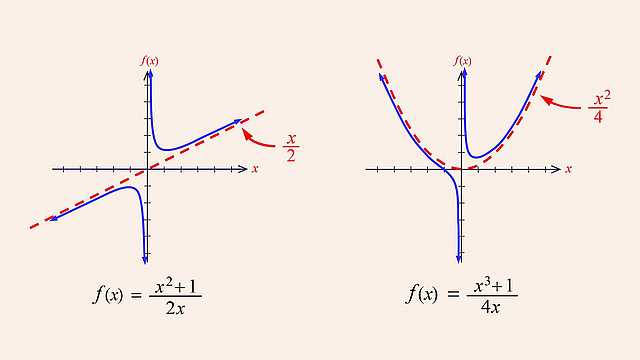92. Rational Functions and Holes
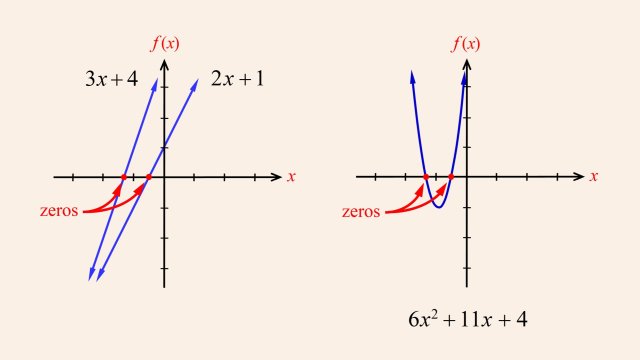
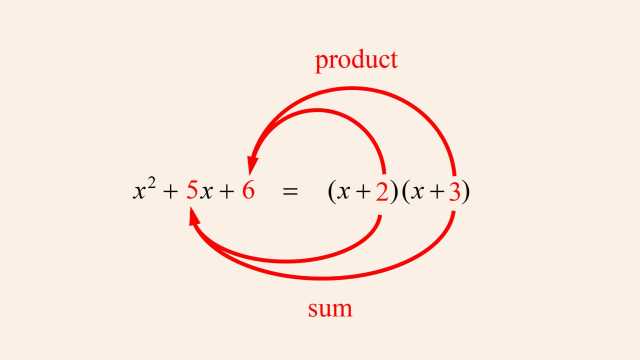
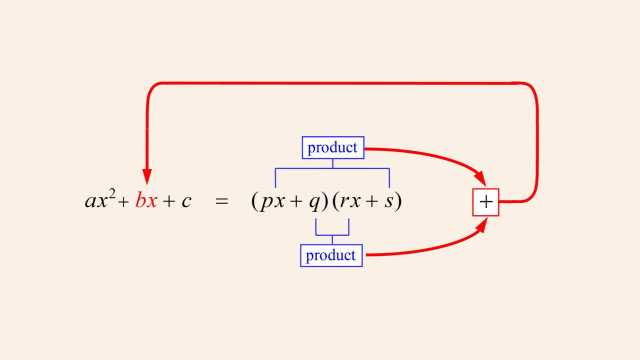
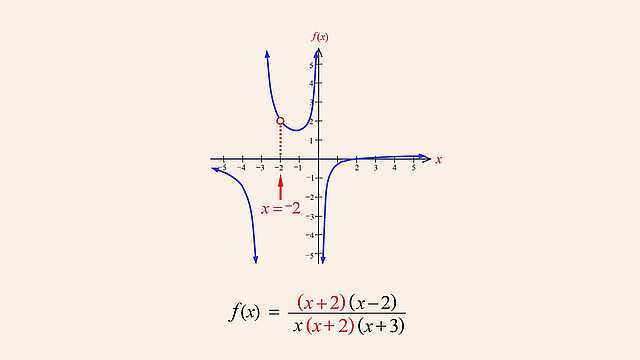
In the previous lecture, we saw examples of x values that cause a rational function's numerator to be zero, where those x values produce x-axis intercepts in the function's graph. We also saw x values that cause denominator zeros that correspond to vertical asymptotes. Since when a rational function's denominator is zero, the function's value is undefined, those x values must be excluded from the function's domain and therefore correspond to missing points in the function's graph. Although, as we saw, those missing points may be associated with vertical asymptotes, in this lecture we will see how when a numerator and denominator zero are both the same, that x value will not correspond to a vertical asymptote, but will simply cause a missing point or "hole" in the function's graph.